IGLOO: Not another RNN
We have published a research paper recently and while it is full of technical details, benchmarks and experiments, we would like to give a more intuitive explanation for this neural network structure. We suggest that the reader checks out the original paper at: https://arxiv.org/abs/1807.03402
A Keras implementation is available at: https://github.com/redna11/igloo1D
Dealing with sequences using Neural Networks
Until Recently Neural networks have been the go-to structure once there was a notion of sequence in a machine learning task. As is well documented, there are issues with vanishing gradients given the recurrent nature of the RNN. Historically the LSTM and the GRU had been the most used RNN structures but recently new improved cells such as the IndRNN, the QRNN, the RWA and a few more have been presented. The improve in terms of speed and convergence on the original cells.
The main idea of all those cells is that the data is processed sequentially.
Besides this, a new structure known as the Temporal Convolutional Network (TCN) can be used to analyze sequential data. The TCN uses 1D convolutions as well as dilated convolutions in order to find a representation for sequences. The paper by (Bai et al., 2018) – An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling gives more details.
Since that initial attempt using convolutions to deal with sequences, the way was open for new methods to emerge.
IGLOO
We know that 1D convolutions applied to sequences return feature maps indicating how the sequence reacts to various filter. Given a kernel size K*, K filters and using a causal 1D convolution (so that at time T, only data up to time T is available) each time step finds a representation with a vector . Each item in this vector represents the activations for each filters for this time step. The full feature map F1 is of size (T,K).
Usual Convolutional Networks then apply another convolution to this initial convolution and returns a second, deeper (in the sense that it is further away from the input) feature map. This second convolutional can be seen as learning relationships between contiguous patches of the feature map. Usual Convnets continue stacking layers this way. The Temporal Convolution network (TCN) structure for example, uses dilated convolutions to reduce the overall depth of the network while aiming at having the deeper layers as large a receptive field as possible, i.e. get higher layers to have as global a view as possible with respect to the initial input. Since the higher layers are connected to all the inputs, it is then up the training process to make the information flow upwards.
The IGLOO structure works differently. After the initial convolution, rather than applying a second convolution layer to F1, we gather p slices on the first axis out of the T available (a typical value of p is 4) which we then concatenate to obtain a matrix H of size (p,K). Those p slice can come from nearby areas or from far away areas, therefore bringing together information from different parts of the feature map. As such one can say that IGLOO exploits non-local relationships in the initial feature map F1. An amount L of those large patches is collected to produce a matrix of size (L,p,K).This matrix is then multiplied point-wise by a trainable filter of the same size. One way to look at this operation is that the filter learns relationships between non-contiguous slices of F1. We then add up together each elements resulting from the point-wise multiplication on the last and the penultimate axis to find a vector U of size L. We also add a bias to this output. As such there will be L biases. A non-linearity such as ReLU is applied (this step is not necessary). As a result we obtain a vector U which will represent the sequence and can then be fed to a Dense Layer and be used for classification or regression. In total, we train (L.K.p + L) parameters (not including the initial convolution C1).
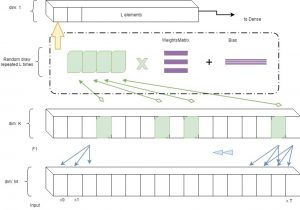
While convolutional networks are all about exploiting local information in a pyramidal fashion, IGLOO tries to gather information from the whole input space. Intuitively, convnets apply successive layers of convolution to an input sequence or image and each layer represents the information with a different level of granularity because each layer further away from the input data has a larger receptive field. IGLOO has direct access to different regions of the input data, so does not need to entirely rely on this pyramidal structure. In essence, it tries to exploit similarity between different parts of the input space to find a representation that can be used for regression or classification.
A Thought Experiment
For example let’s imagine the following thought experiment. We are given sequences with 100 time steps and 10 features, i.e. a matrix of size (100,10). Some sequences have an identical vector of size 10 included in the first 50 time steps, and in the last 50 time steps. Some other sequences do not have any repeating vectors. The goal of this machine learning task would be to train on a large number of example (on a training set) and then be able to correctly identify those sequences which have a repeating element (Class 1) and those which do not (Class 0) given a test set. If choosing at random, we get it right 50% of the time.
How would the RNN deal with the task? The RNN has an internal memory which keeps track of important information required for the error to be minimized. As such , the RNN would deal with each element of the sequence one after the other and keep track of the presence of duplicates or not.
How would IGLOO deal with the task? Image that in the training set, for the very first sample, there are identical vectors at indices 1 and 51. Then while gathering random patches, IGLOO will be dealing with vectors (0,1,10,25), (20,40,60,80) or (1,51,10,3) (It can be set to work with 1000’s of such patches). In the latter case the trainable filter applied to this patch will react strongly by outputting a large positive number and so that the network will learn that if the vector at the 1st index and the vector at the 51 index are identical, then the representation found for the sequence should be of class 1. Then at test time, if the vectors at index 1 and 51 are identical, the network now knows that it should classify as being of class 1.
While this task is fairly simple, some moderately more involved ones are presented in the research document.
Longer Memory with the Copy Memory Task
This task was initially introduced in (Hochreiter and J. Schmidhuber, 1997). We are given a vector of size T+20, where the first 10 elements G=[G0, G1, .., G9] are random integers between 1 and 8, the next T-1 elements are 0’s, the following element is a 9 (which serves as a marker), and the following 10 elements are 0’s again. The task is to generate a sequence which is zero everywhere except for the last 10 items which should be able to reproduce G. The task A can be considered a classification problem and the loss used will be categorical cross entropy (across 8 categories). The model will output 8 classes which will be compared to the actual classes.
Experiments show that for than 1000 time steps, RNNs have difficulties to achieve convergence on this task because partly of the vanishing gradient issue. Since IGLOO looks at a sequence as a whole, it does not suffer from the same drawbacks.
Table 1-b. Task A – COPY MEMORY – IGLOO model. Time to reach accuracy >0.99 in seconds.
| T size (L) | Time in seconds | Params |
| T=100 (300) | 12 | 80K |
| T=1000 (500) | 21 | 145K |
| T=5000 (2500) | 52s | 370K |
| T=10000 (7000) | 61s | 1520K |
| T=20000 (10000) | 84s | 2180K |
| T=25000 (15000) | 325s* | 3270K |
It appears that IGLOO can achieve convergence for sequences of more than 25,000 time steps. There are no RNN in the literature capable of achieving this.
While NLP tasks usually use sequences of less than 1000 steps, there are areas where long sequences are common. For example EEG data and sound waves. The paper includes an experiment with EEG data.
Faster Convergence with the Grammar Task
Closely following (Ostemeyer et al., 2017), we use this task to make sure that IGLOO can represent sequences efficiently and not just sets. To be successful at this task, any neural net needs to be able to extract information about the order in which the elements of the sequence appear. Based on an artificial grammar generator we generate a training set which includes sequences which follow all the predefined grammar rules and are classified as correct and we generate sequences with an error, which should be identified as invalid. As a result of the grammar generator, sequences such as: BPVVE, BTSSSXSE and BPTVPXVVE would be classified as valid and sequences such as: BTSXXSE,TXXTTVVE and BTSSSE would be classified as invalid.
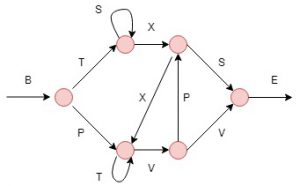
In this case the sequences are only 50 times steps long and have 7 features. The experiment records how long it takes to reach 95% accuracy on the test set using different models.
| Model (hidden) | Time (s) | Params |
| RWA (186) | 1025 | 71,000 |
| LSTM (128) | 384 | 69.900 |
| CuDNNLSTM (128) | 90 | 70,400 |
| CuDNNGRU (148) | NC | 70,000 |
| IndRNN (2*154) | 59 | 73,000 |
| TCN (7*14) | NC | 68,000 |
| IGLOO (500, 2 stacks) | 14 | 76,000 |
It appears that IGLOO is faster on this experiment than other RNN cells tested, and especially faster that the CuDNNGRU cell which is an optimized version of the normal GRU.
Conclusion
We have introduced a new style of neural networks dealing with sequences by exploiting non local similarities. From benchmarks, it seems that it is better than normal RNNs at dealing with very long sequences and at the same time it is faster.
While benchmarks are good to make sure that an idea makes sense in principle, trying out IGLOO out in the wild will allow to understand whether it can be used as a drop-in replacement in some cases.
The Keras/tensorflow code for the structure is provided so it is really a matter of swapping the RNN cell for an IGLOO cell and see if the magic happens. We encourage readers to report on their findings.


